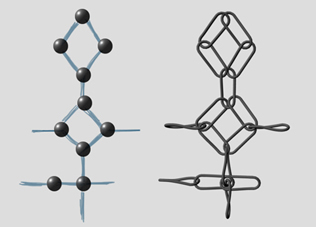
You know quite a lot about knots now. But we haven’t achieved any bondage yet. As you probably anticipate, knowing knots is not enough. But we are much closer than you think. What we need now is a powerful process that can turn any sketch into a real bondage. As this process will rely on our previous results, let us summarize them a little bit.
A bondage is a closed loop.
Elementary knots can be straight, crossed or zeroed
All knots have branches with double rope ends
Complex Knots are black boxes. We have 21 regular knots to pick from.
Knots are closed and made of groups.
Now let’s go! No need to wait any longer!
Let’s draw a sketch, place some knots and see what separates us from the bondage we intended.
= = =
After the sketch is done and the knots are placed, don’t you feel obliged to connect all those knots together? I sure do!!!
As an example let’s just do it. There is no need for any knot there. Let’s just connect them!
And… Here you go!
Done.
Congratulations!!! You’ve just obtained … an unachievable set of closed loops.
You may feel disappointed right now. But actually you’ve just made a big step forward to the solution.
Now WHAT does this experiment mean?
It just means that our process could be complete if we could merge those loops together.
I propose you to study this situation and find the way to do it!
= = =
Closed loops standing apart from each-other are just virtually connected by an elementary knot : the Zero type knot.
Connecting the loops just means you have to replace this 0 knot by a +1 or a -1 type!!!
As you can see in the following, replacing one 0 knot between two closed loops will result in a merged continuous loop.
But merging and merging is not always successful… Replacing twice a 0 knot by a +1 knot would split the ropes again!
And same thing would occur if you replace two 0 knots by -1 ones!
Here you go! You just proved the solution to a very tricky situation : When 2 loops are connected already and you want to connect them again, you shall use a connection of a different type to avoid the rope to split.
In some cases, 2 complex knots facing each-other will unavoidably result in an unconnected portion.
The solution here is obviously to replace one of the knots by another one from the table, that has the same number of branches.
"Draw" and learn even more
Complementary rules
Knots can be very complex. A nice way to reduce complexity is to draw them as black boxes. |
|
|
We can say that 2 links are basically in interaction through 2 knots of type 0 (non-binding) as shown in the following examples :
|
= |
|
Well if we want the links to merge, we just have to replace one of these 0-type knots by a +1 or -1 type. (Let's say the one in the back).
|
or |
|
What if the links interact already? This deserves a few sketches but again the result is immediate. Links interacting through one given type of elementary knot will merge (or stay merged) if the second interaction is of a different type. In other words if the new interaction is of the same type than the existing one, they will split. We shall call this rule "The Complementary Rule". You can see here below, how 2 links split if linked twice with the same elementary type.
|
or |
|
On the left hand side, two links split when linked twice with a +1 knot. On the right hand side, two links split when linked twice with a -1 knot. You can now know in advance whether 2 links will merge or split depending on the elementary knots that you use.
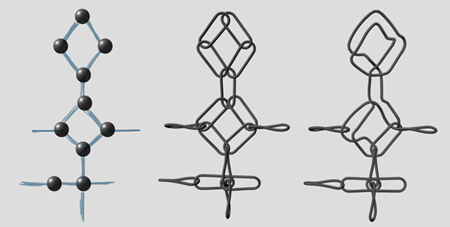
You are now armed to theoretically solve any merging situation; which means you can do any bondage, although it has not been proved scientifically yet. The first thing you have to do is draw it, then place the links. Let the algorithm guide your decisions. A recursive method can be used to attach the links to eachother until your bondage is totally continuous. Here to the right, the unfinished but quite advanced process; from initial drawing on its way to a fully continuous rope bondage. |
|
|
As you noticed, we are not yet drawing knots but rather " simplified connexions" that only tell if the knot is of type +1, 0 or -1. The aesthetics side of it has not been discussed so far... And THAT is a totally different story.
We'll talk about it now.